Update: subsequently republished at Jezebel as "An Incredibly Detailed Super Statistical Hunger Games Survival Analysis".

April 11, 2012

Whenever a new fad  takes over pop culture, social scientists take note. They host conferences, teach courses, and write popular pieces trying to tie the newest thing to their favorite area of research. Consider this post a humble attempt to take that trend to its epic, nerdtastic next level.

As a student of epidemiology and economics I feel duty-bound to apply my cursory knowledge of statistics to the novel natural cohort presented in the Hunger Games novel, as documented by author Suzanne Collins. I present a Hunger Games survival analysis: in a Cox proportional hazards model, which covariates are associated with the odds (or hazard ratios) being ever in your favor? A taste of what's to come:

The agenda:

1. an explanation of the Hunger Games and facts relevant to this analysis
2. a snappy literature review of peripherally-related things other scholars have written on the subject
3. construction and presentation of data set
4. do the Gamemakers rig the draw? an analysis of expected lottery outcomes in scenarios differing by tessera and demographic trends
5. the main event: a Cox proportional hazard model to explore predictors of survival time in the 74th annual Hunger Games.

(Spoiler alert: there will be book spoilers throughout this post. I haven't read the second and third books yet, so please don't spoil them for me or others in the comments. I look forward to analyzing their data as well, and the integrity of this very important research will be enhanced if I can pre-specify the hypotheses I'll test before I've observed the outcomes. Data-mining is not the  fanboy way.)

1. What are the Hunger Games? For the woefully unaware, Suzanne Collins' Hunger Games is aptly summarized by that scholarly redoubt, Wikipedia:

[The Hunger Games] is written in the voice of sixteen-year-old Katniss Everdeen, who lives in a post-apocalyptic world in the country of Panem where the countries of North America once existed. The Capitol, a highly advanced metropolis, holds hegemony over the rest of the nation. The Hunger Games are an annual event in which one boy and one girl aged 12 to 18 from each of the 12 districts surrounding the Capitol are selected by lottery [as "tributes"] to compete in a televised battle in which only one person can survive.

Other facts relevant to this analysis: All children in Panem register for the Hunger Games lottery once a year, and all registrations stay in until you age out (after age 18). So a 12 year old is in a minimum of one time, a 13 year old is in a minimum of twice, etc. The Capitol keeps most districts in near-starvation conditions, so the remedy for many families is to apply for tesserae, a yearly allocation of food that necessitates adding your name to the lottery an additional time. In terms of welfare policy, tessera (plural) are a kind of conditional in-kind transfer of goods (more).

If a child requests one tesserae annually they will have two lottery entries at age 12, four at age 13, and so on. A child requesting five tessera per year will be entered six times at age 12 and on up to a whopping 42 entries at age 18. This is the situation one of the main characters, Gale, faces at the beginning of the book.  Matt Yglesias worried this scenario would lead to runaway tessera inflation, but that shouldn't be a problem as eligibility is apparently capped by number of family members -- Gale takes out five tessera annually to support his five family members.

Still, the odds that any given child will be selected are relatively low -- and even lower in districts with large populations -- but it is the fear that really controls the population. Psychology research helps explain why the Games are so terrible to the citizens of Panem. A little Prospect Theory here:  people are loss averse, and they overweight the likelihood of rare events. The Capitol regime also knows that once children are selected from each district, Prospect Theory predicts that citizens will have a new "reference point" (they assume their tributes will be killed) and thus see victory in the Games as a gain to be celebrated, rather than merely the maintenance of the status quo (the tribute being alive) that existed before the annual lottery.

Also notable are the "Careers," or tributes from wealthy districts who have been trained from early childhood to compete in the Games. Regardless of who is picked by lottery from their district, one of the Careers will volunteer. (There is obvious room for fruitful anthropological inquiry into this subculture.)

This should relieve the fear of the Games in their districts, though it is unclear whether the districts are able to maintain this system because they are wealthy, or whether the districts are wealthy because their citizens work free of the fear of the Games and any impact on demographic trends the fear of losing children might have. This is also an important area for study, but the endogeneity problems and problematic historical data are a challenge worthy of Acemoglu and Robinson.

2. Obligatory literature review

In addition to the aforementioned tesserae inflation post by Matt Yglesias, Matt also  wrote "The Economics of the Hunger Games" where he asks and answers his own question in the subtitle: "could any real country have an economy like Panem's? Actually, yes." In that piece he uses the Hunger Games to illustrate Acemoglu and Robinson's distinction between inclusive vs. extractive institutions.

Next up is Erik Kain's Five Economic Lessons of the Hunger Games, in Forbes. His lessons are 1) Markets Are More Efficient Than Command Economies, 2) Globalism Only Works If You Ditch The Extraction Model, 3) Economic Inequality Is Bad For Business, 4) War Drains Economic Resources, and 5) Technology Can Be Used For Good Or Evil. I particularly liked this note:

Furthermore, arbitrarily picking Districts to supply only one type of good to the Capitol means that human capital is badly mismanaged. Nothing about being born in District 12 makes you a better miner, any more than being born in District 2 makes you a better soldier.

Ironically, a flourishing market economy likely would have meant a far more wealthy populace in the Capitol as well. Hundreds of years in the future, we should expect to be far wealthier and more technologically advanced than even the wealthiest citizens of Panem.

This reminds me that our current world economy is in some ways very much like Panem, with massive restrictions to cross-border flow of human capital (i.e., people). Michael Clemens of the Center for Global Development has done some valuable work exploring the economic benefits (to everyone, not just the immigrants) of allowing greater migration.

Finally, there's "Probability and Game Theory in the Hunger Games," by Michael A. Lewis, writing at Wired. Lewis explores the lottery process -- and I think here he's quite wrong, but more on that below in the nitty-gritty of my analysis. Then he moves on to game theory, using the decision within the Hunger Games of whether to sleep or not sleep as an illustration of Prisoner's Dilemma. I think his analysis of the dilemma the children face and how it prompts them to form alliances is correct. But as I read Lewis' article I thought of another, related dilemma:

The people of any given District could game the system by all agreeing to put in for the maximum quantity of tessera without hurting anyone. A simplified example: if the entire child population of District 12 consisted of 10 fourteen-year-old kids and they all have the minimum three entries, there are 30 entries total and each child has a 3/30 (or 1 in 10) likelihood of being chosen.

But if each of the kids agrees to request two tessera annually, they would each have nine entries ate age fourteen, making their likelihood of selection 9 out of 90... which is still 1 in 10. In other words, so long as everyone agrees to increase tessera selection simultaneously, everyone benefits in terms of extra food and no one is more likely to be selected.

So why doesn't this happen? Two reasons: first, Capitol may require the tessera requests to be private and otherwise block coordination efforts amongst the population in a given district. Without perfect information about what others are actually getting, Gale could tell everyone he put in for five tessera (to decrease their marginal risk from requesting more, which would make him less likely to be selected!) while actually only putting in for three.

Second, income inequality exacerbates problems as wealthy families would not opt into such a coordinated system because they do not need the extra food -- if everyone were equally poor andable to coordinate such a scheme might work.

3. Construction of data set

The iteration of the Hunger Games depicted in the novel is the 74th annual, meaning that there have been 1,776 participants to date and 75 winners (two in year 74). It sure would be nice to have all that data! Alas, Collins only documents the 74th Games, but I think there is still some interesting analysis to be done.

I began by perusing the novel for information about each character. Later I discovered that much of the information I needed was already available through the Hunger Games Wiki, helpfully compiled by people even nerdier than me (and with less binding time constraints). Here's how the data looks in Stata (version 11.2), which I used for the survival anaylsis:

To allow others to check and improve upon my analysis, I've made the data available for download in a Google Doc spreadsheet, along with my Stata code in a Google Document (which contains instructions for downloading and importing the data into Stata).

On methodology: I assigned each tribute a unique ID (1 through 24) and names, where available. The other variables in the data set are:

• District (1 through 12)
• Sex (0 = male, 1=female)
• Age (12 through 18)
• Volunteer (0 = no, 1 = yes)
• Career (0 = no, 1 = yes)
• Gamemakers' Rating (5-11 or 3-11, depending on methodology described below)
• Rank (order in which they exited the games, from 1st for Katniss and Peeta to 14th for those who died in the initial bloodbath)
• Winner (0 = no, 1 = yes for Peeta and Katniss)
• Alliance (0 = not formed, 1 = formed an alliance)

In cases where data from the book and novel conflicted (as was the case with rank for a few tributes) I went with the book. In cases where data is available in the movie that isn't in the book (as with age), I did use the movie data.  District, sex, age, rank, and winner were unambiguous.

For the alliance "dummy" (not necessarily an indicator of intelligence) variable, those who formed an alliance are represented by 1 (this includes both the Careers alliance and the short-lived Rue-Katniss alliance) and 0 if they survived the bloodbath but did not form an alliance. I thought it would be unfair to assign an alliance value to those who died in the bloodbath, as they may well have formed one had they survived. Also, Katniss is notable for being the only volunteer in the data set who was not also a Career.

The Gamemakers' ratings should be good predictors of survival time, as they represent expert judgments based on knowledge of the previous games and inside knowledge of fighting ability. However, precise ratings were only available for the nine named characters: Marvel, Glimmer, Cato, Clove, Foxface, Thresh, Rue, Peeta, and Katniss. The variable "rating" gives the other tributes missing values.

However, the book also notes that the Careers scored mostly between 8 and 10, whereas the other non-Career tributes scored a 5 "on average". So I added another variable "rating_ave" that assigns a 9 to the Careers with missing values and a 5 to non-Careers with missing values. I also created "rating_rand," which creates plausible ratings by using the generator at Random.org to give random integers between 8 and 10 for the Careers and between 3 and 7 for the non-Careers. This allows the rating data to be analyzed using any of these three methods.

4. Do the Gamemakers rig the draw?

Building off Michael A. Lewis' thoughts on the odds of being selected in the lottery, I wanted to explore the age distribution of the tributes. How can we tell whether the Gamemakers are actually rigging the vote, to bring in younger or more compelling tributes to enhance the drama of the Games? Luckily we have enough information to explore this question a bit.

When you use Stata to tabulate the tributes by age, you find a few funny things. For instance, seven (29.2%) of the 24 tributes are age 15, and 6 (25.0%) are age 16, which seem high to me. But in a random process like a lottery -- and with small numbers of children actually chosen -- it can be difficult for human intuition to distinguish between random variation and something else. For that, we need statistical analysis. Graphically (using Excel), the distribution of the proportion of tributes by age looks like this:

How does this compare to the expected distribution of tributes based on the increasing risk of being selected in any given year? Astute readers will have already notice that I'm including all 24 tributes here, whereas eight of them (Katniss plus 7 Careers) volunteered and were not randomly selected. So breaking the tributes down by volunteer vs. non-volunteer status yields this graph:

The red bars represent counts of non-volunteers, which should be due to random selection based on their number of entries in the lottery. Here's where I differ with Lewis' analysis at Wired. Lewis presents this graph of increasing probability of selection as children age:

As Lewis notes, this is from an example where all the children are of the same age, and the total pool of children gets smaller as children get selected or age out. This is a bit silly, and doesn't really help us understand the lottery dynamics. A more realistic scenario would involve cohorts that are roughly the same size each year, so that the same number of children enter the pool and exit the pool in any given year. This rests on the assumption that demographic trends in Panem are fairly stable -- after all, it has existed with the same system in place for 74 years, and Capitol would likely avoid incentivizing rapid demographic changes that could destabilize the situation.

Discounting tesserae for now, if a cohort of children enters and has one entry at 12, two at 13, and so on, the probability that a child from a particular age will be selected in any given year increases arithmetically: 3.6% at age 12, 7.1% at age 13, 10.7% at age 14, 14.3% at age 15, 17.9% at age 16, 21.4% at age 17, and 25% at age 18. In other words, just by nature of the accumulating lottery entries as you age, one out of four lottery draws should be an 18 year old. Using these proportions and multiplying them by the 18 tributes actually selected by lottery, I get the blue line on the graph below, which represents the expected number of children from each age if the lottery is completely random:

By comparing the red bars (non-volunteer children) to the blue expected line, you can see the apparent difference in outcomes. However, we haven't yet tested whether these differences are statistically significant or could simply happen by chance.

[A side note on tesserae: Lewis rightly notes that it is difficult to analyze further without understanding why some families select tesserae and others do not. I don't think the problem is quite as difficult as that. Choosing tesserae is likely dependent on income so it makes sense to assume that a certain percentage of the population in each District doesn't request it at all, whereas others require one, two, or more tessera every year to survive (we know that Gale took at five every year.) But that shouldn't matter when analyzing the probability of a given age being selected unless the likelihood of choosing tesserae differs systematically (in the whole population) by age. In other words, people who put in for one tessera at age 12 are likely to continue requesting one tessera per year, and if they increase or decrease that request the change will be offset by changes in requests from other citizens. If 10% of the population requests the maximum tesserae every year but that doesn't change as the children age (because family size remains constant) then children remain at constant risk based on their age. I modeled a few scenarios in Excel to convince myself of this, but I won't present those here. Thus, I'm assuming that on average the number of tesserae requested is determined by income but not by age, as need stays constant over time.]

Given those assumptions, tesserae can be discounted as a major factor impacting lottery selection. On an individual level it's still bad to be poor and thus need tesserae, and it's still bad to get older and thus have your name in the lottery more times, but on the population level we can model the probability of selection of a given age.

To do so I used a Chi-square test in Stata, testing to see whether there's a difference between the observed counts and the expected counts, the blue line in the graph above. Stata's built-in functionalities don't quite cut it, you'll need to install the tab_chi package (just use the command "findit tab_chi") which was created by Nicholas Cox. Then you just enter this command to perform a Chi-square test: "chitesti 1 0 1 5 4 3 2 \ 0.571428576 1.142857136 1.714285712 2.285714288 2.857142864 3.428571424 4". This yields a Pearson Chi-square statistic of 6.4958 (P=0.370).

This indicates that the difference between the age distribution in the 74th Hunger Games is not different (with a traditional statistical significance threshold of P=0.05) from the expected age distribution given an arithmetic increase in lottery names by age and the tesserae assumptions outlined above. Thus, the available data does not support the hypothesis that the Gamemakers rigged the draw in the 74th games. Of course, this test depends on the assumptions regarding tesserae and demographics explained above. And ideally we'd have data from all the games, which would allow us to detect more subtle patterns with a larger sample size. This analysis works for the 74th games, but external validity -- whether we can extrapolate from these results to all instances of the Games -- may be problematic.

5. Survival analysis: which covariates are associated with longer survival in the Games?

Survival analysis is quite important in epidemiology. Kaplan-Meier graphs are commonly used in the medical literature to visually represent the difference in survival over time between two different groups -- often treatment vs. control. Survival analysis can be used with any outcome, not just death, so long as the data you have is measure time that passes until an event.

When these statistical tool are used in economic and other non-health data, they're often described as "event history analysis" as the vocabulary of survival analysis makes less sense. However, it should be morbidly clear that the language of survival analysis works just fine with the Hunger Games scenario. In fact, it's a perfect opportunity to explore survival analysis as we have data for how long each tribute survived in the arena, as well as a number of covariates measured at the beginning of the contest.

I won't go into much coding detail on the survival analysis, but Stata users can access my .do file (linked above) to replicate the analysis. Rather, I'll present the results graphically where possible. Graphs are pretty. First, you can see how the Nelson-Aalen cumulative hazard estimator increases with time:

Next I ran a few univariate analyses of what I thought might be important predictors. In the following Kaplan-Meier graphs the y axis shows the proportion of tributes surviving at a given point in time. Since our unit of time is days, you see a "step down" each time someone dies. Here's a graph showing the survival by sex:

Not much difference. On the first day both male and female drop from 1.00 (everyone surviving) to close to 0.50. On the second day the male line doesn't budge from 0.50, but the female line drops down to 0.50: this is the demise of the District female, killed by Peeta and Cato in the book but by Glimmer in the film, as noted at the Hunger Games Wiki). The last blue step down -- on day 17 -- is Cato. In this graph each step is the same height (0.083 = 1/12) because the numbers of male and female tributes are the same, but in subsequent graphs this isn't always true. (An aside on gender: Lewis' article also points out that it's unclear how Capitol deals with transgender citizens.)

Next, by Careers vs. non-Careers, the graph included as a teaser at the beginning of this post:

The Careers get a head-start at the bloodbath, but things even out by around day 10. At least in this particular iteration of the Games, the do not fare better overall than the non-Careers.

Graphing by age is messy because there are too many categories (and Kaplan-Meier graphs don't work with continuous variables) so I grouped the tributes into three age categories:

I ran several more of these bivariate analyses, and then finally fit a Cox proportional hazards model, yielding this Stata output:

The only statistically significant effect (at the traditional and arbitrary cutoff of P<0.05) comes from the Gamemakers' rating variable. The career dummy variable just misses the cutoff (P=0.065) and might be significant if we had a larger sample size and saw similar trends in the data, but effect is in the wrong direction: holding other things constant (sex, age, and Gamemakers' rating), Careers do less well than non-Careers! Of course, this only happens in this analysis because Peeta and Katniss (but mostly Katniss) are awesome.

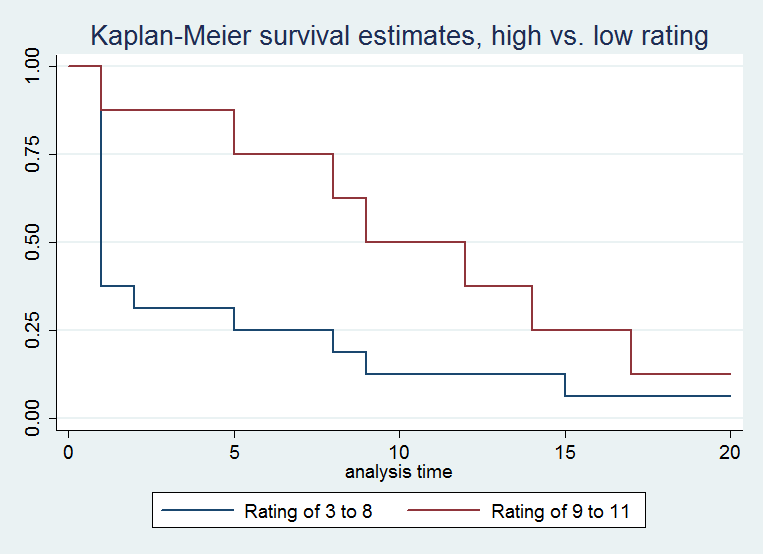
Because it would be disappointing to end on a non-visual note, I created a dichotomous low vs. high rating variable based on whether tributes had scores of 3 to 8 or 9 to 11 on the rating_rand variable. Here you can see just how different the survival outcomes for the low and high ability groups are:

My interpretation of this is that the Gamemakers know what they're doing when they assign the ratings. They've been doing this for years, so they give scores that are so accurate that they're actually better predictors of survival time than whether a tribute is a volunteer, a Career, male or female, or forms an alliance. Pretty impressive.

An alternate and more cynical interpretation is that the Gamemakers are concerned about their own reputations and thus engineer the games so as to confirm their ratings, occasionally killing off players who do better or worse than expected based on the ratings, all so that the Gamemakers can look like they knew what they were doing all along. Unfortunately, the political system of Panem ranks so slow on Freedom House's annual scores that we simply can't tell what's going on behind the scenes at all. To cut through their lies we simply need more data.

(P.S. Feel free to run your own analysis of the data, but please credit and link to me. After all, a social science community lacking incentives for researchers to share the data they gather is no community at all.)

Updates: I changed the links to the data and .do file to be to Google Docs rather than files hosted on this site. Thanks to my classmate Kristin for some coding suggestions (yay "peer review"!). I also added the results table from the regression model and some commentary related to it. And then I added some clarifying comments throughout the post but haven't noted every minor change.